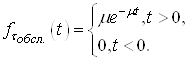
Рефераты по авиации и космонавтике
Рефераты по административному праву
Рефераты по безопасности жизнедеятельности
Рефераты по арбитражному процессу
Рефераты по архитектуре
Рефераты по астрономии
Рефераты по банковскому делу
Рефераты по биржевому делу
Рефераты по ботанике и сельскому хозяйству
Рефераты по бухгалтерскому учету и аудиту
Рефераты по валютным отношениям
Рефераты по ветеринарии
Рефераты для военной кафедры
Рефераты по географии
Рефераты по геодезии
Рефераты по геологии
Рефераты по геополитике
Рефераты по государству и праву
Рефераты по гражданскому праву и процессу
Рефераты по делопроизводству
Рефераты по кредитованию
Рефераты по естествознанию
Рефераты по истории техники
Рефераты по журналистике
Рефераты по зоологии
Рефераты по инвестициям
Рефераты по информатике
Исторические личности
Рефераты по кибернетике
Рефераты по коммуникации и связи
Рефераты по косметологии
Рефераты по криминалистике
Рефераты по науке и технике
Рефераты по кулинарии
Рефераты по культурологии
Рефераты по зарубежной литературе
Рефераты по логике
Рефераты по логистике
Рефераты по маркетингу
Реферат: Системи масового обслуговування з очікуванням без обмеження на довжину черги
Реферат: Системи масового обслуговування з очікуванням без обмеження на довжину черги
Системи масового обслуговування з очікуванням без обмеження на довжину черги
1. Системи масового обслуговування з очікуванням
Багатоканальні
СМО з обмеженою чергою. Нехай є система СМО, що має ![]() каналів. Кожна заявка
надходить до СМО, починає обслуговуватись, коли хоча б один із каналів вільний.
Якщо усі канали зайняті, тоді заявка потрапляє у накопичувач, де чекає
звільнення хоча б одного із каналів. Нехай черга у накопичувачі обмежена числом
каналів. Кожна заявка
надходить до СМО, починає обслуговуватись, коли хоча б один із каналів вільний.
Якщо усі канали зайняті, тоді заявка потрапляє у накопичувач, де чекає
звільнення хоча б одного із каналів. Нехай черга у накопичувачі обмежена числом
![]() . Якщо,
один із каналів звільняється, заявка надходить на обслуговування до звільненого
каналу по черзі, з якою заявка надійшла у СМО. Якщо заявка застане усі канали і
усі місця у накопичувачі зайнятими, то вона втрачається. Потім припускатимемо,
що вхідний потік заявок також пуассонівського з параметром
. Якщо,
один із каналів звільняється, заявка надходить на обслуговування до звільненого
каналу по черзі, з якою заявка надійшла у СМО. Якщо заявка застане усі канали і
усі місця у накопичувачі зайнятими, то вона втрачається. Потім припускатимемо,
що вхідний потік заявок також пуассонівського з параметром ![]() , а потік обслугованих
заявок також пуассонівський с параметром
, а потік обслугованих
заявок також пуассонівський с параметром ![]() . Тоді система може знаходитись у
станах
. Тоді система може знаходитись у
станах ![]() Причому
Причому
![]() – це
стани, коли немає черги, тобто відповідно
– це
стани, коли немає черги, тобто відповідно ![]() – всі канали вільні,
– всі канали вільні, ![]() – один
зайнятий, … ,
– один
зайнятий, … , ![]() – усі
– усі ![]() каналів зайняті,
каналів зайняті, ![]() - усі канали зайняті і
одна заявка в черзі, … ,
- усі канали зайняті і
одна заявка в черзі, … , ![]() – стан, коли всі
– стан, коли всі ![]() каналів і всі
каналів і всі ![]() місць у
накопичувачі зайняті, тобто заявка, що надходить в такий момент втрачається.
Можна графічно на рис. (1) стрілками вказати усі переходи від стану до стану, а
над стрілками ймовірності переходів за час
місць у
накопичувачі зайняті, тобто заявка, що надходить в такий момент втрачається.
Можна графічно на рис. (1) стрілками вказати усі переходи від стану до стану, а
над стрілками ймовірності переходів за час ![]() , якщо
, якщо ![]() малий.
малий.

Рисунок 1
Якщо
порівняти СМО з відмовами і СМО з обмеженою чергою, то зрозуміло, що для
ймовірностей переходу ![]() , коли
, коли ![]() , ми одержуємо такі ж
диференціальні рівняння як і рівняння системи без черги.
, ми одержуємо такі ж
диференціальні рівняння як і рівняння системи без черги.
Отже
потрібно скласти рівняння для перехідних ймовірностей, коли ![]() .
.
Нехай
![]() .
Враховуючи властивості простіших потоків і формулу Смолуховського-Чепмена
.
Враховуючи властивості простіших потоків і формулу Смолуховського-Чепмена
![]() ,(1)
,(1)
де ![]() – функція що задовольняє умові
– функція що задовольняє умові 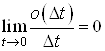 .
.
![]() , (2)
, (2)
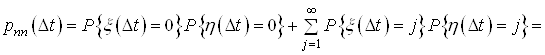
![]() , (3)
, (3)
де як
і раніше ![]() число
заявок, що надходять до СМО за час
число
заявок, що надходять до СМО за час ![]() ,
,
а ![]() – число
заявок, що обслуговані за час
– число
заявок, що обслуговані за час ![]() .
.
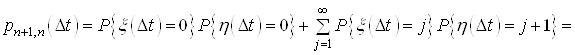
![]() (4)
(4)
Тепер врахуємо (2), (3 і (4) до (1)
![]()
Віднімемо
від обох частин останньої рівності ![]() та розділимо на
та розділимо на ![]()
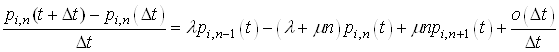
Перейдемо
до границі в обох частинах, коли ![]()
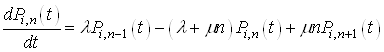 (5)
(5)
Тепер,
продовжуючи аналогічні міркування, можна одержати рівняння для обчислення
перехідних ймовірностей із стану до стану, коли ![]() , де
, де ![]()
Враховуючи формулу Смолуховського-Чепмена, а також властивості простішого (пуассонівського) потоку можна записати:
![]()
![]() (6)
(6)
Далі за властивістю стаціонарності і ординарності, маємо:
![]() , (7)
, (7)
![]() , (8)
, (8)
![]() . (9)
. (9)
Врахуємо (7), (8) і (9) до (6).
![]()
В
останній рівності
віднімемо від обох частин ![]() і розділимо на
і розділимо на ![]() .
.
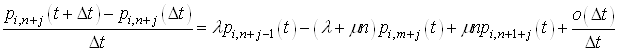
А
тепер перейдемо до границі в обох частинах, коли ![]() , тоді
, тоді
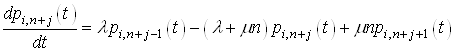 (10)
(10)
де ![]() .
.
Останнє
рівняння системи, для визначення перехідних ймовірностей ![]() , містить
, містить ![]() :
:
![]()
Враховуючи ті ж самі властивості стаціонарності і ординарності простіших (пуассонівських) потоків, одержимо:
![]() , (11)
, (11)
![]() . (12)
. (12)
Якщо підставити (11) і (12) у рівність (10), тоді матимемо:
![]() .
.
Якщо
відняти від обох частин останньої рівності ![]() , а далі розділити на
, а далі розділити на ![]() , тоді запишемо
, тоді запишемо
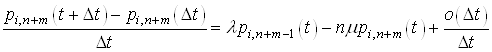
Тепер
обчислимо границі від обох частин, якщо ![]() :
:
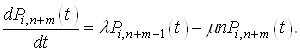 (13)
(13)
Таким
чином отримуємо систему диференціальних рівнянь для обчислення ![]() – ймовірностей переходу
від стану
– ймовірностей переходу
від стану ![]() до
стану
до
стану ![]() СМО
з чергою, що має скінченне число місць в накопичувачі:
СМО
з чергою, що має скінченне число місць в накопичувачі:
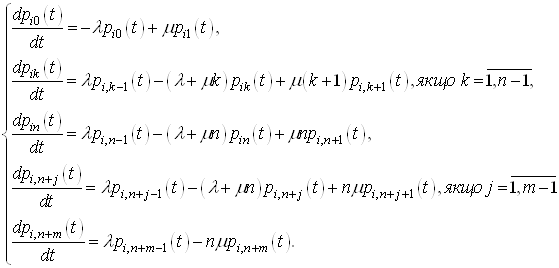 (14)
(14)
Якщо
спостерігати СМО достатньо довгий час ![]() , тоді розв’язок системи (14)
можна знайти, якщо позначити
, тоді розв’язок системи (14)
можна знайти, якщо позначити ![]() (фінальні ймовірності) у вигляді:
(фінальні ймовірності) у вигляді:
 (15)
(15)
Система
(15) є лінійною, однорідною, алгебраїчною системою з невідомими ![]() . Для того, щоб знайти
єдиний розв’язок системи (15) необхідно додати умову
. Для того, щоб знайти
єдиний розв’язок системи (15) необхідно додати умову
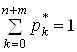 .(16)
.(16)
Раніше
було доведено, що для усіх ![]() діє формула:
діє формула:
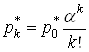 , де
, де 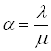
![]()
Тепер
розглянемо ![]() -е
рівняння системи (15) і обчислимо
-е
рівняння системи (15) і обчислимо ![]() ,
,
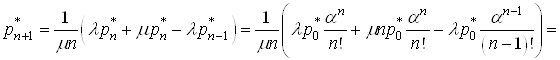
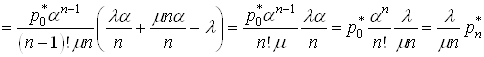 .
.
Отже,
одержали зв’язок ![]() і
і ![]()
![]() де
де 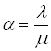 (17)
(17)
Нехай
формула (17) є правильною для ![]() . Необхідно довести, що вона
правильна і для
. Необхідно довести, що вона
правильна і для ![]() . Для цього із системи (15)
візьмемо рівняння з номером
. Для цього із системи (15)
візьмемо рівняння з номером ![]() , отже
, отже
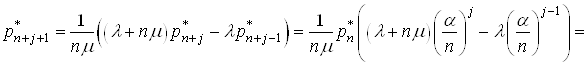
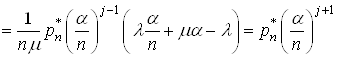 ,
,
тобто
 .(18)
.(18)
Тепер
потрібно перевірити, що (18) правильна і для ![]() . Для цього необхідно взяти
останнє рівняння системи (15), з нього маємо
. Для цього необхідно взяти
останнє рівняння системи (15), з нього маємо
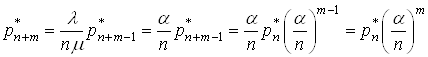 .(19)
.(19)
Таким чином, якщо порівняти (18) і (19), можна записати:
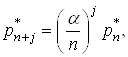
![]() .(20)
.(20)
Отже,
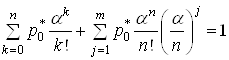 , звідки
можна знайти
, звідки
можна знайти ![]() , тобто, якщо врахувати формулу
суми геометричної прогресії
, тобто, якщо врахувати формулу
суми геометричної прогресії  ,
,
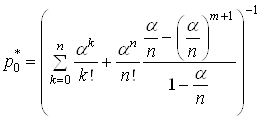 (21)
(21)
2. Багатоканальні СМО з очікуванням без обмеження на довжину черги
система масове обслуговування очікування черга
Для
того, щоб скласти рівняння для перехідних імовірностей у випадку, коли СМО має
безліч місць у накопичувачі, треба із системи (14) викреслити останнє рівняння
і покласти ![]() .
Питання існування фінальних ймовірностей для такої системи пов’язано з умовами,
які дають можливість виконуватися рівності
.
Питання існування фінальних ймовірностей для такої системи пов’язано з умовами,
які дають можливість виконуватися рівності  , а це, якщо врахувати
, а це, якщо врахувати
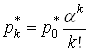 ,
, ![]() ,(22)
,(22)
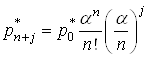 ,
, ![]() (23)
(23)
то (21) дає
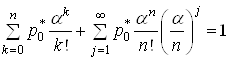 .(24)
.(24)
Другий
доданок у (24) є нескінченний ряд, який утворений із геометричної прогресії із
знаменником ![]() .
Отже, для того, щоб він був збіжний, потрібно, щоб
.
Отже, для того, щоб він був збіжний, потрібно, щоб ![]() . Це є умовою, для існування
фінальних імовірностей
. Це є умовою, для існування
фінальних імовірностей ![]() , коли
, коли ![]() . З точки зору практичного
використання цієї умови необхідно, щоб середня кількість заявок, які надходять
до системи за середній час обслуговування однієї заявки одним каналом, була
строго меншою ніж кількість каналів. Тоді формула (21) спрощується:
. З точки зору практичного
використання цієї умови необхідно, щоб середня кількість заявок, які надходять
до системи за середній час обслуговування однієї заявки одним каналом, була
строго меншою ніж кількість каналів. Тоді формула (21) спрощується:
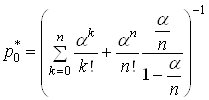 при умові
при умові ![]() (25)
(25)
Основні
характеристики СМО з очікуванням. Зупинимось на таких характеристиках СМО з
очікуванням, коли довжина черги нескінченна, як середнє число заявок у черзі,
середнє число заявок у СМО, функція розподілу часу очікування початку
обслуговування, середній час перебування заявки
у СМО.
1. Середнє число заявок у черзі
Оскільки
число заявок в черзі є випадковою величиною із значеннями
0, 1, 2, … і ймовірностями відповідно ![]() , тоді середнє число заявок у
черзі є математичне сподівання цієї величини, тобто:
, тоді середнє число заявок у
черзі є математичне сподівання цієї величини, тобто:
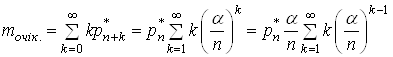 .(26)
.(26)
Для
того, щоб знайти суму ряду 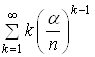 , спочатку знайдемо суму ряду
, спочатку знайдемо суму ряду 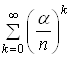 , який утворено
від геометричної прогресії із знаменником
, який утворено
від геометричної прогресії із знаменником ![]() , тобто
, тобто  . Оскільки останній ряд є
степеневий ряд відносно
. Оскільки останній ряд є
степеневий ряд відносно ![]() , то він рівномірно збігається для
усіх
, то він рівномірно збігається для
усіх ![]() ,
тому його можна почленно диференціювати по
,
тому його можна почленно диференціювати по ![]() . Тоді матимемо
. Тоді матимемо
 (27)
(27)
Тепер врахуємо (27) у рівності (26):
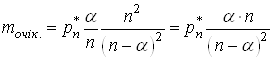 ,(28)
,(28)
де 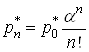 і
і ![]() обчислюється
за формулою (25).
обчислюється
за формулою (25).
Середнє число заявок у СМО обчислюється:
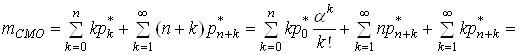
(29)
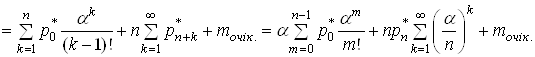 .
.
Оскільки
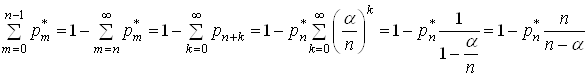
тоді (29) можна спростити:

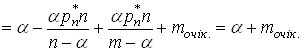 .
.
Таким чином середнє число заявок у СМО є
![]() ,(30)
,(30)
тобто складається із середнього числа заявок, що находять за середній час обслуговування однієї заявки і середнього числа заявок, що очікують у черзі.
3. Функція розподілу часу очікування початку обслуговування
Нехай
![]() є
випадкова величина часу, який заявка чекає у СМО до початку обслуговування.
Необхідно визначити функцію розподілу цієї величини, тобто
є
випадкова величина часу, який заявка чекає у СМО до початку обслуговування.
Необхідно визначити функцію розподілу цієї величини, тобто ![]() . Якщо використати
визначення функції розподілу, то матимемо:
. Якщо використати
визначення функції розподілу, то матимемо:
![]() .
.
Знайдемо
![]() при
умові, що час очікування обслуговування
при
умові, що час очікування обслуговування ![]() є випадкова подія, коли усі
канали вільні, чи коли зайнятий хоча б один з
є випадкова подія, коли усі
канали вільні, чи коли зайнятий хоча б один з ![]() каналів, тобто
каналів, тобто

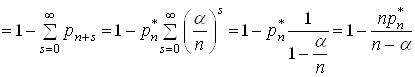 .
.
Таким чином
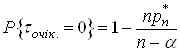 (31)
(31)
Тепер
обчислимо ![]() .
По-перше, позначимо ймовірність
.
По-перше, позначимо ймовірність ![]() того, що за час
того, що за час ![]() обслуговуватиметься
більше ніж
обслуговуватиметься
більше ніж ![]() заявок,
при умові, що зайняті усі
заявок,
при умові, що зайняті усі ![]() каналів. Крім того, оскільки
потік обслуговування заявок є пуассонівським з параметром
каналів. Крім того, оскільки
потік обслуговування заявок є пуассонівським з параметром ![]() , то ймовірність
обслуговування
, то ймовірність
обслуговування ![]() заявок одним каналом обчислюється
за формулою
заявок одним каналом обчислюється
за формулою 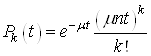 .
.
Якщо
на обслуговуванні два канали, тоді кожний канал обслуговує одну заявку
незалежно від другого. Отже ймовірність того, що ![]() заявок будуть обслужені двома
каналами обчислюється за формулою суми двох незалежних подій
заявок будуть обслужені двома
каналами обчислюється за формулою суми двох незалежних подій
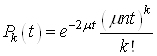 .
.
Далі,
продовжуючи аналогічні міркування, можна записати таку формулу для ймовірності
обслуговування за час ![]()
![]() заявок, якщо
заявок, якщо ![]() каналів зайняті:
каналів зайняті:
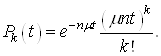 (32)
(32)
Таким чином, якщо врахувати (32)
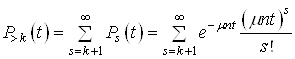 (33)
(33)
Обчислимо
ймовірність ![]() за умови (33):
за умови (33):
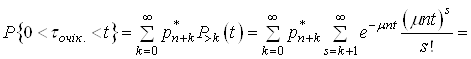
(34)
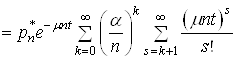 .
.
В
останній рівності поміняємо порядок сумування змінних ![]() і
і ![]() . Тоді (34) можна записати у
вигляді:
. Тоді (34) можна записати у
вигляді:

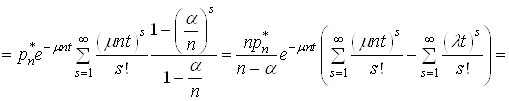
 .
.
Тепер
можна записати значення ![]() :
:
 (35)
(35)
Враховуючи (31) і (35) до рівності (28) маємо вираз для функції розподілу часу очікування початку обслуговування у вигляді
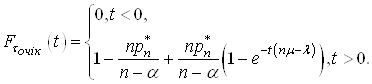 (36)
(36)
Вираз (36) можна спростити і тоді:
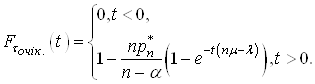 (37)
(37)
Випадкова
величина ![]() не
є дискретною, бо в точці
не
є дискретною, бо в точці ![]() і 1 функція розподілу
і 1 функція розподілу ![]() має розрив.
Якщо ввести функцію
має розрив.
Якщо ввести функцію 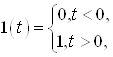 що має похідну
що має похідну 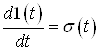 , тоді можна записати
щільність розподілу часу очікування обслуговування
, тоді можна записати
щільність розподілу часу очікування обслуговування ![]() , тобто
, тобто
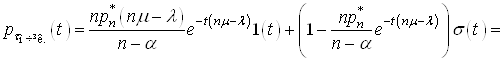
(38)
 ,
,
де 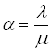 .
.
4. Середній час очікування початку обслуговування
Якщо врахувати (38) і формулу обчислення математичного сподівання випадкової величини, тоді можна обчислити середній час очікування початку обслуговування:
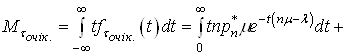
(39)
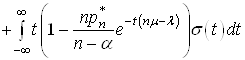 .
.
Відомо,
що 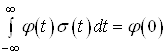 , тому
другий інтеграл у (39) дорівнює нулю, тоді
, тому
другий інтеграл у (39) дорівнює нулю, тоді
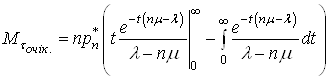 .(40)
.(40)
Оскільки
для існування фінальних ймовірностей достатньо, щоб ![]() , тоді
, тоді 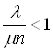 , звідки
, звідки ![]() . Враховуючи це в (40), отримаємо:
. Враховуючи це в (40), отримаємо:
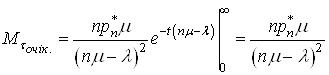 .(41)
.(41)
5. Середній час перебування заявки у СМО
Позначимо
середній час перебування заявки в СМО через ![]() . Середній час перебування заявки
в системі складається із часу очікування обслуговування і часу, що йде на
обслуговування, тобто
. Середній час перебування заявки
в системі складається із часу очікування обслуговування і часу, що йде на
обслуговування, тобто
![]() ,
,
тоді
![]() .
.
Враховуючи
(41) і те , що 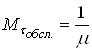 , маємо
, маємо
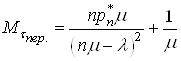 . (42)
. (42)
6. Функція розподілу випадкового часу перебування заявки у СМО
![]()
(43)
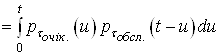 ,
,
де ![]() – щільність
розподілу випадкового часу очікування обслуговування, що обчислюється за
формулою (38), а
– щільність
розподілу випадкового часу очікування обслуговування, що обчислюється за
формулою (38), а ![]() – щільність розподілу випадкового
часу обслуговування.
– щільність розподілу випадкового
часу обслуговування.