Реферат: Финансовые расчеты

Сибирский институт финансов и банковского дела

Кафедра: Финансы и кредит

Контрольная работа

по дисциплине: Финансовые расчеты

Вариант №3

Выполнил: студентка группы СЗ-96

Бурдюгова О.В.

Проверил: кандидат экономических наук

Текутьев Владимир Евгеньевич

Новосибирск 1998 г.

Раздел 1. Проценты

Задача №1

Ссуда в размере 1,000 д. е. предоставлена 5 февраля и должна быть погашена 5 мая с уплатой простых процентов по годовой ставке 70%. Какую сумму должен возвратить заемщик при начислении:

обыкновенных процентов с приближенным числом дней ссуды;
обыкновенных процентов с точным числом дней ссуды;
точных процентов;

Решение

Дано

P = 1,000 S = P(1+in)

i = 0.7 n = t/T

S = ?

А) метод обыкновенных процентов с приближенным числом дней:

t = 24+30+30+4 = 88

T = 360

n = 0.244 1

S = 1,000(1+0.7*0.244) = 414.8 д.е

Б) метод обыкновенных процентов с точным числом дней:2

t = 24+31+30+4 = 89

T = 360

n = 0.247

S = 1,000(1+0.7*0.247) = 419.9 д.е.

В) метод точных процентов:

t = 24+31+30+4 = 89

T = 365

n = 0.244

S = 1,000(1+0.7*0.244) = 414.8 д.е.

1 Все вычисления в данной работе производятся до 3 –го знака после запятой, если другое не оговорено отдельно.

2 Во всех задачах в данной работе при вычислений n = t/T используется метод обыкновенных процентов с точным числом дней, если другое не оговорено условием задачи.

Задача №2

Вклад в сбербанк в сумме 200,000 рублей помещен под 70% годовых. Рассчитать сумму вклада и начисленные проценты:

через 7 месяцев;
через 2.5 года.

Чему равны множители наращения в обоих случаях?

Решение

Дано

P = 200,000 руб. 1) S = P(1+in)

n1 = 7/12 года I = S - P

n2 = 2.5 года qs = S/P

i = 0.7 2) S = P(1+i)na (1+nbi)

S-?, I-?, qs-?, qc-? где na + nb = n

na – целая часть периода

nb – дробная часть периода

при n < 1 начисляются простые проценты

S = 200,000(1+0.583*0.7) = 221620д.е.

I = 221620 – 200,000 = 21620

qs = 221620/200,000 = 1.108

если n > 1 и не целое число то проценты начисляются по комбинированному способу

S = 200,000(1+0.7)2 (1+0.7*0.5) = 491300 д.е.

I = 491300 – 200,000 = 291300

qc = 491300/200,000 = 2.457

Задача №3

Выразить при помощи эффективной ставки доходность следующих операций:

некоторая сумма помещается на 1 – месячный депозит под 80% годовых;
некоторая сумма помещается на 3 – месячный депозит под 90 % годовых.

Какая из двух операций эффективней?

Дано

j1 = 80% ; m1 = 12 ; n1 = 1/12

j2 = 90% ; m2 = 4 ; n2 = 0.25 ie = (1+j/m)mn - 1

Вычислим периодическую ставку при 1- месячном и 3-х месячном депозитах:

j1/m1 = 80/12 = 6.667% - на месячном депозите

j2/m2 = 90/4 = 22.5% - на 3-х месячном депозите

Непосредственное сравнение 6.667% за 1 месяц и 22.5% за 3 месяца не позволяет сравнить эффективность этих операций. Поэтому для сравнения эффективности этих операций вычислим годовую эффективную ставку для каждой из них:

ie = (1+0.8/12)12 – 1 = 1.17 = 117% - для 1 - месячного депозита

ie = (1+0.9/4)4 – 1 = 1.252 = 125.2% - для 3-х месячного депозита

Сравнив годовые эффективные ставки мы видим, что операция с одномесячным депозитом эффективнее операции с 3-х месячным депозитом при данных процентных ставках.

Задача №4

Вексель на сумму 1,200,000 д.е. со сроком уплаты 1 ноября учитывается в банке 1 сентября по учетной ставке 28 %. Какую сумму получит владелец векселя (без уплаты комиссионных )? Какова величина дисконта?

Решение

Дано

S = 1,200,000 Sk = S - D

ds = 0.28 где Sk – сумма полученная

Sk - ? , D - ? клиентом.

D = Snds

n = t/T

n = t/T = 61/360 = 0.169

D = 1,200,000*0.169*0.28 = 56,784 д.е.

Sk = 1,200,000 – 56784 = 1,143,216 д.е.

Задача№5

За какой срок при начислении сложных процентов удваивается сумма вклада, помещенного под 25% годовых, если начисление производится:

ежегодно;
ежеквартально;
ежемесячно.

Решение

Дано

i = 0.25 1) S = P(1 + i)n , где S = 2P

n - ? 2) и 3) S = P(1 + j/m)mn , где S = 2P

2P = P(1+0.25)n ; сократим обе части уравнения на P

2 = 1.25n ; прологарифмируем обе части уравнения

lg2 = lg1.25n = nlg1.25

n = lg2/lg1.25 = 0.301/0.097= 3.103 года

сделаем проверку: пусть P = 1000 , тогда S = 1000(1+0.25)3.103 = 1998.535

при вычислении до 4-го или 5-го знака после запятой получатся более точное значение n.

2P = P(1+j/m)mn

2 = 1.0634n

lg2 = 4nlg1.063

n = lg2/(4lg1.063) = 2.84 года;

2P = P(1+j/m)mn

2 = 1.02112n

n = lg2/(12lg1.021) = 2.79 года;

Задача №6

Какая годовая ставка сложных процентов обеспечивает удвоение вклада до востребования за 1.17 года, если проценты начисляются:

ежеквартально;
ежемесячно;
ежедневно.

Решение

Дано

n = 1.17 S = P(1+j/m)mn

j - ? где S = 2P

2P = P(1+j/4)4.68

2 = (1+j/4)4.68

(21/4.68 - 1)m = j

j = 4(21/4.68 - 1) = 0.64 = 64%

2P = P(1+j/12)14.04

j = 12(21/14.04 - 1) = 0.605 = 60.5%

2P = P(1+j/360)427.05

j = 360(21/427.05 - 1) = 0.506 = 50.6% (вычисления производились до 4-го знака после запятой).

Задача №7

По первоначальному варианту соглашения 1 сентября должно быть уплачено 20,000,000 д.е., 1 декабря еще 10,000,000 д.е. Стороны договорились объединить эти платежи одним. Консолидированный платеж должен быть произведен 1 ноября. Какой должна быть его сумма, если соглашение предусматривает начисление простых процентов из расчета 70% годовых.

Решение

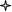
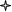
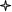
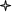Дано S1 S2

S1 = 20,000,000 1.09 1.10 1.11 1.12

S2 = 10,000,000

n1 = 2/12 S

n2 = 1/12

S - ? 1.11

S = S1(1+n1i) + S2(1+n2i)-1

S = 20,000,000(1+2/12*0.7) + 10,000,000(1+1/12*0.7)-1 = 31880000д.е.

Задача №8

Два векселя: на сумму 2000000 д.е. (срок платежа 10.09) и 5000000 д.е. (срок платежа 01.11) заменяются одним с пролонгацией до 15.11. Найти сумму нового векселя, учетная ставка при пролонгации 28%.

Решение

Дано

S1 = 2,000,000 i = d(1-nd)-1

S2 = 5,000,000 n = t/T

d = 0.28 Snew = S1(1+n1i1) + S2(1+n2i2)

Snew - ?

i1 = 0.28(1 - 65/360*0.28)-1 = 0.295

i2 = 0.28(1 - 14/360*0.28)-1 = 0.283

Snew = 2,000,000(1+0.053) + 5,000,000(1+0.011) = 7161555.1 д.е.

Задача №9

Прогноз годового индекса цен Ip= 2.2. Рассчитать соответствующее значение уровня инфляции за год и в среднем за месяц (в процентах).

Решение

Дано

Ip = 2.2  = Ip – 1

 - ? ср.мес = Ipмес – 1

ср.мес - ? Ipмес = Ip1/m

где m число месяцев в изучаемом периоде.

 = 2.2 - 1 = 1.2 = 120%

Ipмес = 2.21/12 = 1.067

ср.мес = 1.067 - 1 = 0.067 = 6.7%

Задача №10

Во сколько раз возрастут цены за год, если инфляция в среднем за месяц ( в процентах) будет иметь значение ср.мес = 4%.

Решение

Дано

ср.мес = 0.04 ср.мес = Ip1/m - 1

Ip - ?

Ip1/m = 1+ср.мес

Ip = (1+ср.мес)m

Ip = (1+0.04)12 = 1.601 раз

Задача №11

Рассчитать реальную покупательную способность 1,000,000 руб., помещенных на 0.5 года под 108% годовых с ежеквартальным начислением, если среднемесячный уровень инфляции ожидается 4%. Рассчитать реальную доходность данной операции в виде годовой ставки.

Решение

Дано

P = 1,000,000 Sr = S/Ip

j = 1.08 ir = (1+j/m)mn/Ip

m = 4 Ip = (ср.мес +1)m

n = 0.5

ср.мес = 0.04

Sr - ?, ir - ?

Sr = 1,000,000(1+1.08/4)2 / 1.046 = 1275019.76руб.

Ir = [(1+1.08/4)4/1.0412] - 1 = 0.625 = 62.5%

Задача №12

Рассчитать значение номинальной ставки, которая обеспечит реальную доходность операции, равную 30% годовых, от размещения некоторой суммы на 0.5 года с ежеквартальным начислением, если среднемесячный уровень инфляции ожидается равным 4%.

Решение

Дано

ir = 0.3 j = m[(Ip(1+ir))1/m -1 ]

мес = 0.04 Ip = ( мес + 1)12

m = 4

j - ?

Ip = 1.0412 = 1.601

j = 4(1.6491/4-1 ) = 0.804 = 80.4%

Раздел 2. Финансовая рента (аннуитет)

Задача №13

Клиенту банка открыта кредитная линия на 2 года, дающая возможность в начале каждого квартала получать по 5,000,000 д.е., на которые ежегодно начисляются 12%. Рассчитать общую доходность к концу срока.

Решение

Дано

n = 2 S = R/p*[(1+i)n –1] / [(1+i)1/p –1]

i = 0.12 S0= S(1+i)1/p

R/p = 5,,000,000

S0 - ?

S0 = 5,000,000(1.12 2 –1) / (1.12 0.25 –1 )1.12 0.25 = 5,000,000*8.759*1.029 = 45065055 д.е.

Задача №14

В 1984 году в индийском городе Бхопал произошла катастрофа на химическом заводе американской компании ``Union Carbide``, приведшая к гибели около 2000 человек. Компания предложила выплатить семьям погибших в общей сложности 200 млн. $, производя эти выплаты ежегодно равными суммами в течение 35 лет. Если бы индийская сторона приняла эти условия, то какую сумму фирме следовало поместить в банк для обеспечения в течение указанного срока ежегодных выплат, если на средства соответствующего фонда ежеквартально начисляются проценты по ставке 12% годовых.

Решение

Дано

S = 200,000,000 S = R[(1+j/m)mn –1] / [(1+j/m)m –1]

n = 35 A = R[1 – (1+j/m)-mn] / [(1+j/m)m –1 ]

j = 0.12

m = 4

A-?

R = [(1+j/m)m –1] / [(1+j/m)mn –1] S = 0.126/61.692*200,000,000 = 411818.54

A = 411818.54* 0.984 / 0.126 = 3216106.6 $

Задача №15

Определить размер ежегодных взносов, вносимых в конце года, в следующих случаях:

для создания через пять лет фонда в размере 50 млн. д.е.;
для погашения в течение 5-ти лет текущей задолженности, равной 50 млн. д.е.

Процентная ставка – 12%.

Решение

Дано

S = 50,000,000 S = R[(1+i)n –1] / i

A = 50,000,000 A = R[1 – ( 1+i)-n / i

n = 5

i = 0.12

R - ?

Rs = Si / [(1+i)n –1] = 0.12*50,000,000 / (1.125 –1) = 8,000,000 / 1.1 = 7874015.7 д.е

RA = Ai / [1 – (1+i)-n] = 8,000,000 / 0.5239 = 13856812 д.е

Задача №16

Определить срок, за который величина фонда составит 100 млн. д.е., если взносы в фонд в сумме 10 млн. д.е. производятся:

в начале каждого года;
в конце каждого года.

Проценты на взносы начисляются ежеквартально по ставке 12%.

Решение

Дано

S = 100,000,000 S0 = R[(1+j/m)mn –1] / [(1+j/m)m –1] * (1+j/m)m

R = 10,000,000 S = R[(1+j/m)mn –1] / [(1+j/m)m –1]

m = 4

j = 0.12

n - ?

100,000,000 = 10,000,000(1.034n –1)1.126 / 0.126

1.26 / 1.126 = 1.126n –1

2.119 = 1.126n

lg2.119 = nlg1.126

n = 0.326 / 0.052 = 6.3 лет

100,000,000 = 10,000,000(1.1699n –1) / 0.1699

1.699 =1.1699n –1

2.699 = 1.1699n

lg2.699 = nlg1.1699

n = 0.4312 / 0.0681 = 6.3 года

Задача №17

Определить срок, за который текущая задолженность в 100 млн. д.е. может быть погашена ежегодными срочными уплатами по 25 млн. д.е., вносимыми в конце года, если проценты на остаток долга начисляются ежеквартально по ставке 12%. Рассчитать критическое значение величины срочной уплаты такое, при котором платежи лишь погашают проценты, не позволяя погасить основной долг.

Решение

Дано

A = 100,000,000 1) A = R[(1 – (1+j/m)-mn] / [(1+j/m)m –1]

R = 25,000,000 2) S = P + I где I = (1+j/m)mn

m = 4 P = A, n = 1

n - ?

1) A = R[(1 – (1+j/m)-mn] / [(1+j/m)m –1]

A[(1+j/m)m –1] / R = 1 – (1+j/m)-mn

A * 0.126 / R –1 = - (1.03-4)n

0.504 –1 = - 0.888n

-0.496 = -0.888n

lg0.496= nlg0.888

n = -0.305 / -0.052 = 5.6 года

2) S = 100,000,000 * 1.939 = 193900000

I = 93900000

Rкрит = Sкрит[(1+j/m)m –1] / [(1+j/m)mn]; где Sкрит = I

Rкрит = Sкрит = 93900000 д.е.

Раздел 3. Элементы прикладного финансового анализа.

Задача №18

Облигации ГКО номиналом 10,000 руб. продаются за 6 месяцев до погашения по курсу 83. Рассчитать абсолютную величину дохода от покупки 10 облигаций и доходность инвестиций в них по схеме простых и сложных процентов.

Решение

Дано

N = 10,000 K = P/N*100

K = 83 1Y = (N – P)/P*365/t

t = 6 мес. Yc = (N/P)365/ t –1

W10 - ?, Y - ?

P = KN/100 = 8,300

W10 = (N – P)*10 = (10,000 – 8,300)*10 = 17,000 руб.

Y = 1,700/8,300*2 = 0.41 = 41%

Yc = (10,000/8,300)2 –1 = 0.452 = 45.2%

Задача №19

Облигация номиналом 1000 д.е. погашается через 10 лет по номиналу. Она приносит 8% ежегодного дохода. Рассчитать оценку, курс и текущую доходность облигации для условной ставки сравнения 6%.

Решение

Дано

N = 1,000 P = Nq(1 – (1+i)-n) / i + N(1+i)-n

n = 10 K = P / N*100

q = 0.08 Y = Nq / P*100

i = 0.06

P - ?, K - ?, Y- ?

P = 1,000*0.08(1 – (1+0.06)-10) / 0.06 + 1,000*(1+0.08)-10 = 589.333 + 558 = 1147.333 д.е.

K = 1000 / 1447*100 = 69.11

Y = 1000*0.08 / 1447*100 = 5.53%

1В задачах №18 и №19 3-го раздела t – число дней от приобретения ценной бумаги до ее погашения.

Задача №20

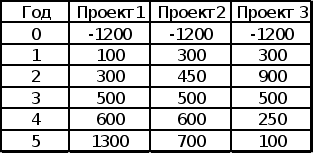
Приведены исходные данные по трем инвестиционным проектам. Оценить целесообразность выбора одного из них, если финансирование может быть осуществлено за счет ссуды банка под 8% годовых.

Динамика денежных потоков

Решение

Для обоснования целесообразности выбора одного из трех предложенных инвестиционных проектов, произведем оценку их эффективности по следующим показателям:

Чистая приведенная ценность NPV = 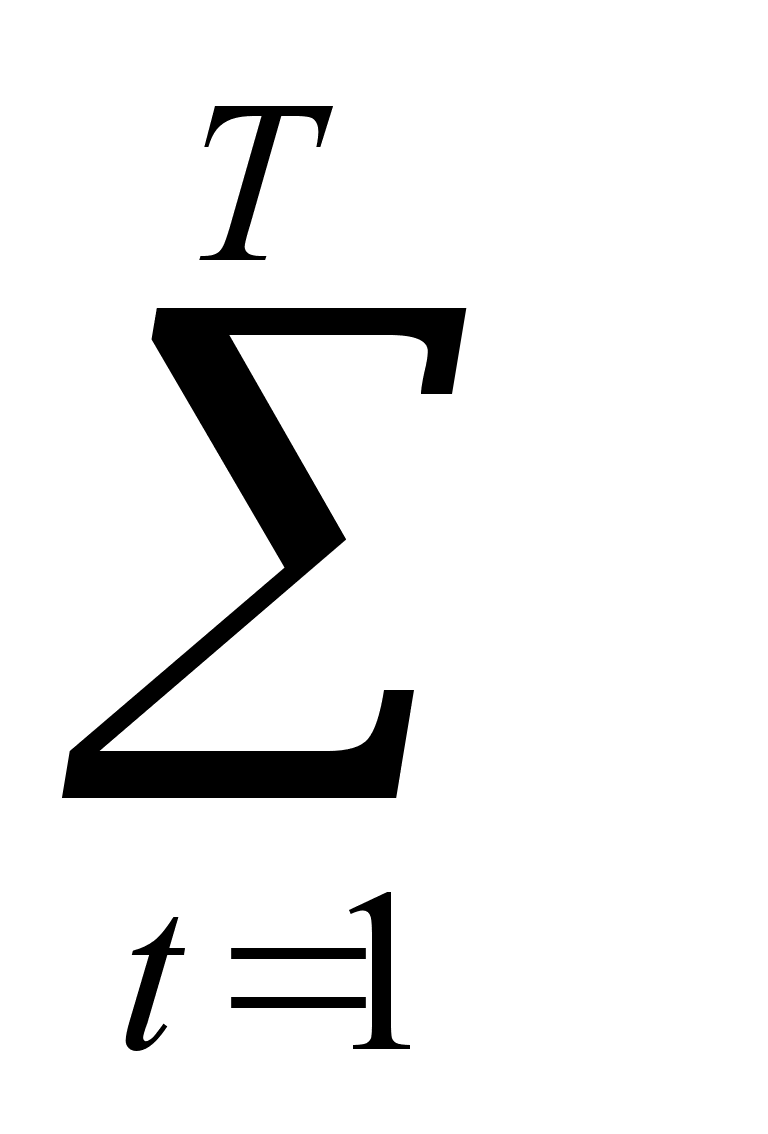Pt(1+i)-t –IC

где t – порядковый номер шага расчета;

Pt – t-й член потока чистых денег;

IC – величина инвестированного капитала;

T – число лет на которое делается расчет.

Индекс прибыльности PI = 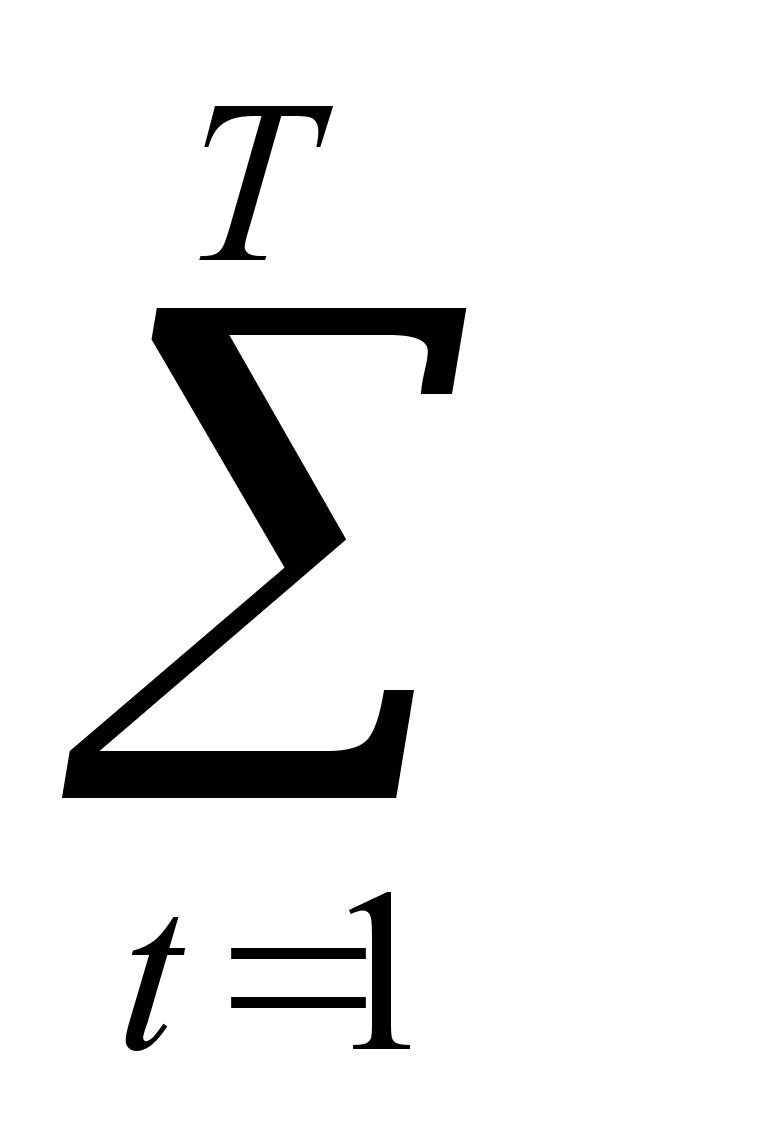Pt(1+i)-t / IC

3. Срок окупаемости PP = tmin, при котором Pt(1+i)-t > IC

Внутренняя ставка доходности IRR = i, при котором 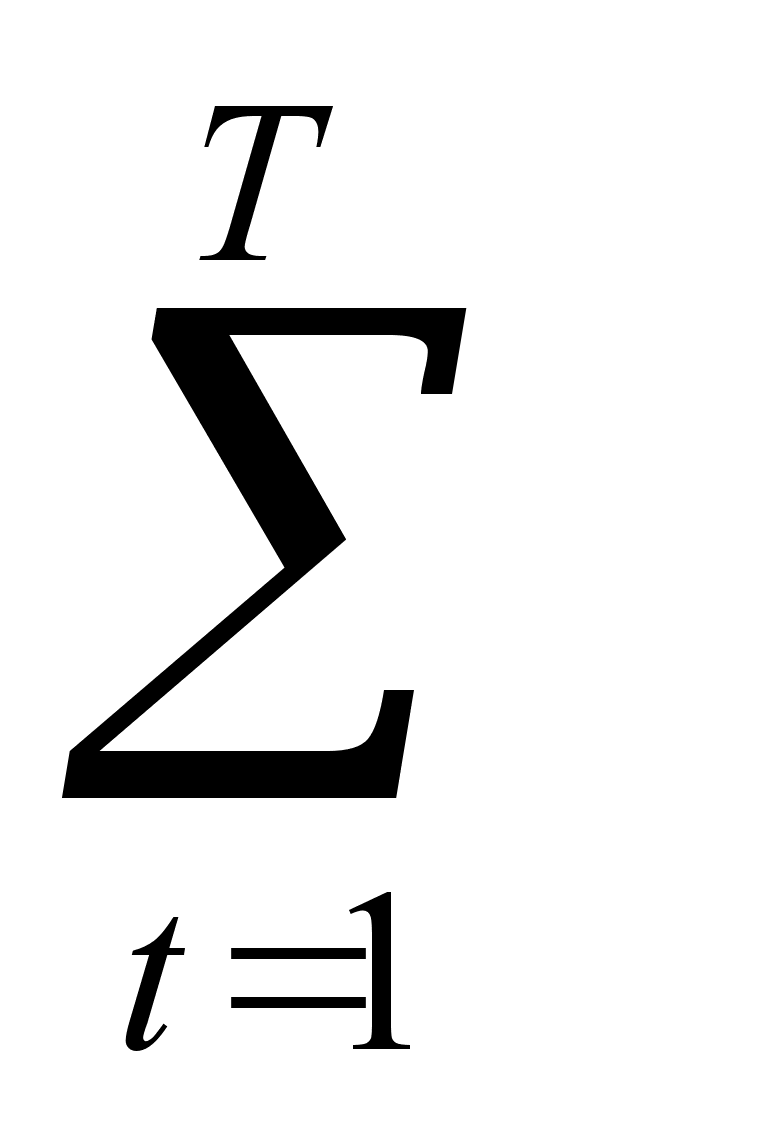Pt(1+i)-t = IC

IRR = i1+(i2 – i1)NVP(i1) / (NVP(i1) – NVP(i2); ( для вычисления IRR возьмем значения i1 = 6%, i2 = 10%)

Речь о целесообразности проекта может быть только при следующих значениях вышеперечисленных показателей: NPV >IC, PI >1, PP – чем меньше, тем лучше, IRR=>i.

При других значениях этих показателей речь об эффективности инвестиционного проекта не ведется. Расчеты всех вышеперечисленных показателей приведены в таблице приложения 1. Из таблицы видно, что наиболее эффективным и более стабильным является проект 2. О стабильности проекта так же можно судить по диаграмме дисконтированного потока чистых денег.